Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Das Geburtstagsparadoxon
Der Professor wettet in der Vorlesung mit den Studierenden, dass mindestens zwei Studierende im Hörsaal am gleichen Tag Geburtstag haben.
- Wir gehen von 365 Tagen pro Jahr aus.
- Das Jahr der Geburt bleibt unberücksichtigt.
Wie groß sind seine Chancen, dass er diese Wette gewinnt, wenn an diesem Tag 40 Studierende anwesend sind?
Zuerst überlegen wir, wie wahrscheinlich es ist, dass zwei Personen an unterschiedlichen Tagen Geburtstag haben: Die erste Person kann an einem beliebigen Tag aus 365 Geburtstag haben. Die zweite Person darf nun nicht mehr an demselben Tag Geburtstag haben, hat also nur noch 364 Tage zur Auswahl.
Das bedeutet, dass die Wahrscheinlichkeit p dafür, dass zwei Personen an zwei unterschiedlichen Tagen Geburtstag haben, folgende ist:
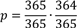
Für drei Personen ist dann die Wahrscheinlichkeit, dass alle drei an unterschiedlichen Tagen Geburtstag haben:
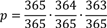
Für n Personen gilt dann:
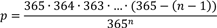
Jetzt fragen wir uns allerdings nicht, wie wahrscheinlich es ist, dass alle Personen an verschiedenen Tagen Geburtstag haben, sondern, wie wahrscheinlich es ist, dass mindestens zwei am selben Tag Geburtstag haben. Hier ist also nach der Gegenwahrscheinlichkeit P gefragt, also Eins minus der Wahrscheinlichkeit, dass alle an unterschiedlichen Tagen Geburtstag haben (P = 1 – p).
Wir erhalten also die Formel:
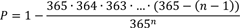
Dem Bruch kann man ansehen, dass er bei steigender Personenanzahl einen immer kleineren Zahlenwert bekommt. Wenn man 1-„einen sehr kleinen Zahlenwert“ nimmt, so bleibt das Ergebnis sehr nah an der Eins. Dies bedeutet eine große Wahrscheinlichkeit.
Wenn wir n = 40 einsetzen, erhalten wir p = 0,89 — sprich eine Wahrscheinlichkeit von 89%, dass mindestens zwei Personen am selben Tag Geburtstag haben. Bereits bei 23 Personen ist die Wahrscheinlichkeit schon knapp über 50%, obwohl 365 Tage zur Auswahl stehen; daher spricht man von einem Paradoxon.

