Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Pascalsches Dreieck
Das Pascalsche Dreieck ist die graphische Darstellung der Binomialzahlen in Form eines Dreiecks (Bildungsgesetz siehe animierte Abbildung). Die Bezeichnung geht auf Blaise Pascal (* 19. Juni 1623 in Clermont-Ferrand; † 19. August 1662 in Paris) zurück, jedoch war diese Form der Anordnung der Binomialzahlen schon weitaus früher bekannt.
Das Pascalsche Dreieck ist extrem vielseitig. Es kodiert nicht nur die Binomialkoeffizienten, sondern auch die Anzahl der k-elementigen Teilmengen einer n-elementigen Menge. Man kann darin die Dreieckszahlen wiederfinden, sowie die Fibonacci-Zahlen oder die Catalan-Zahlen. Und wenn man alle ungeraden Zahlen schwarz und die geraden weiß färbt, ergibt sich eine fraktale Form, das Sierpinski-Dreieck und es gibt noch vieles mehr darin zu entdecken.

1. Aufgabe Binomische Formel
Die Binomialzahlen entsprechen den Koeffizienten in der binomischen Formel n-ten Grades:

Was kodiert die 5-te Zeile im Pascalschen Dreieck?
Ein Koeffizient in der binomischen Formel zählt genau die Anzahl der Monome x4—k yk, was gleichbedeutend ist mit der Anzahl der k-elementigen Teilmengen einer 4-elementigen Menge.
2. Aufgabe Dreickszahlen
Die Bezeichnung Dreieckszahl leitet sich von der geometrischen Figur des Dreiecks her. Insbesondere entspricht die Anzahl der Steine, die man zum Legen eines gleichseitigen Dreiecks benötigt, einer Dreieckszahl.

Als Formel erhält man:

Wo stehen die Dreieckszahlen im Pascalschen Dreieck?
Wie man der Abbildung leicht entnehmen kann, stehen die Dreieckszahlen in der dritten Diagonalen.
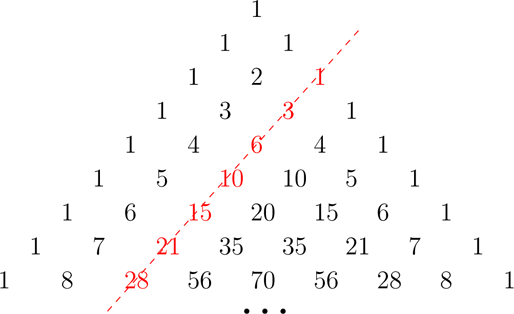
Es folgen Diagonalen mit den Tetraeder-Zahlen, hier stapelt man die Kugeln in Form eines Tetraeders und Pentatop-Zahlen usw.
3. Aufgabe Fibonacci-Zahlen
Das folgende Rätsel machte Leonardo da Pisa, auch Fibonacci genannt (* um 1170 in Pisa; † nach 1240 ebenda), berühmt:
Ein Mann setzte ein Paar Kaninchen in einen allseits ummauerten Ort. Wieviele Kaninchenpaare können innerhalb eines Jahres aus diesem Paar erwachsen, wenn jedes Paar in jedem Monat ein Pärchen als Nachwuchs bekommt und der sich ab dem zweiten Monat ebenfalls vermehrt?
Wir schreiben die Antwort für jeden Monat nacheinander in Form einer Folge auf:

Man erkennt sofort, dass diese Zahlenfolge ein festes Bildungsmuster hat. Jede Zahl ergibt sich als Summe der beiden vorangehenden Zahlen. Diese Folge bezeichnet man als Fibonacci-Folge.
Wo finden sich die Fibonacci-Zahlen im Pascalschen Dreieck wieder?
Wenn man wie in der Abbildung eingezeichnet jeweils die Zahlen auf den „flachen“ Diagonalen aufaddiert, erhält man tatsächlich die Fibonacchi-Zahlen.
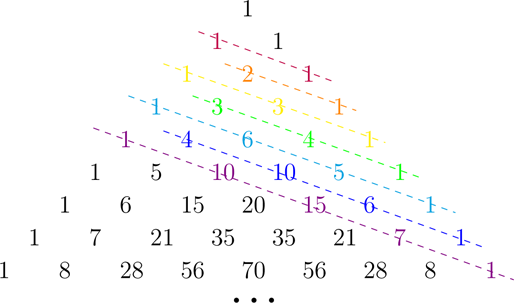
Wir nähern uns aber auch noch einer anderen bedeutenden Zahl: dem Goldenen Schnitt. Genauer genommen strebt das Verhältnis zweier aufeinander folgenden Zahlen der Fibonacci-Folge gegen den Goldenen Schnitt.

