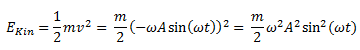Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Der harmonische Oszillator am Beispiel eines Federpendels Teil 2
Ein kleiner Exkurs zum harmonischen Oszillator:
Der harmonische Oszillator ist ein sehr wichtiges Konzept in der Physik: Mit Hilfe des harmonischen Oszillators lassen sich viele Phänomene in der Physik beschreiben. Ein Beispiel ist die Beschreibung des Federpendels, bei dem eine Masse an einer Feder schwingt, oder der elektromagnetische Schwingkreis, bestehend aus Spule und Kondensator. Auch Molekül- und Gitterschwingungen lassen sich mit Hilfe des harmonischen Oszillators beschreiben. Wesentliche Bestandteile der Festkörperphysik und spektroskopische Eigenschaften von Stoffen können so erklärt werden. In der Quantenphysik wird ein quantisierter harmonischer Oszillator verwendet um quantisierte Zustände zu beschreiben.
Zur Aufgabe:
Diese Aufgabe dient dazu Ihnen einen Einblick in die Physik zu ermöglichen. Sie beschäftigt sich mit dem harmonischen Oszillator am Beispiel eines Federpendels. Hierbei wird ein idealisiertes Experiment formal beschrieben und wichtige Größen berechnet und anschließend physikalisch gedeutet. Die Aufgabe ist etwas umfangreicher und bietet die Möglichkeit selbst zu knobeln. Lassen Sie sich nicht abschrecken, wenn eine Antwort auf Anhieb nicht richtig ist, sondern versuchen Sie das Ergebnis nachzuvollziehen!
Knobeln Sie gerne und machen Ihnen schwierige Rechnungen Spaß?
Wollen Sie lernen, wie man aus Formeln physikalische Zusammenhänge erkennen kann?
Dann ist für sie das Studium der Physik genau richtig!
Betrachten Sie ein Federpendel bestehend aus einem Körper der Messe m, welcher an einer Feder mit einer Federkonstante k hängt. (Hierbei handelt es sich um ein ideales Pendel ohne Reibung.) Wird das Pendel aus seiner Ruhelage um die Stecke A ausgelenkt und dann losgelassen, so beginnt dieses um seine Ruhelage zu schwingen.
Berechnung der Energie des Federpendels
Bei einem Federpendel wird periodisch kinetische Energie in potenzielle Energie umgewandelt. Dabei ist die Gesamtenergie konstant (ideales Pendel mit Vernachlässigung der Reibung).
Aufgabe: Berechnen Sie mit dem Ergebnis für die Geschwindigkeit v und die Beschleunigung a aus dem ersten Teil der Aufgabe die Gesamtenergie des Pendels, welche sich als Summe aus kinetischer und potenzieller Energie zusammensetzt. Gehen Sie dabei davon aus, dass die Anfangsphase gleich Null ist (φ0 = 0). In der nächsten Box finden Sie eine Formelsammlung mit den Ergebnissen aus Teil 1 (Geschwindigkeit v und Beschleunigung a) und weiteren Formeln, die Sie für die Rechnung benutzen können. In den darauf folgenden Boxen sind die einzelnen Rechenschritte zur Kontrolle aufgeführt. Schnappen Sie sich hierfür Zettel und Stift und los geht’s!
Hinweis: Diese Aufgabe ist ein Beispiel für eine sehr schwierige und anspruchsvolle Aufgabe. Neben dem Versuch die Aufgabe selbst zu lösen, sind auch das Verstehen der Lösung und das Nachvollziehung der Rechnung Teil der Aufgabe. Probieren Sie selbst aus, welche Teile der Aufgabe Sie selbstständig lösen können, welche Teile für Sie nachvollziehbar sind und an welchen Stellen Sie sich vorstellen können die Aufgabe in einer Gruppe zu diskutieren.
Woher kommt die Formel für die potenzielle Energie?
Zunächst einmal muss unterschieden werden zwischen:
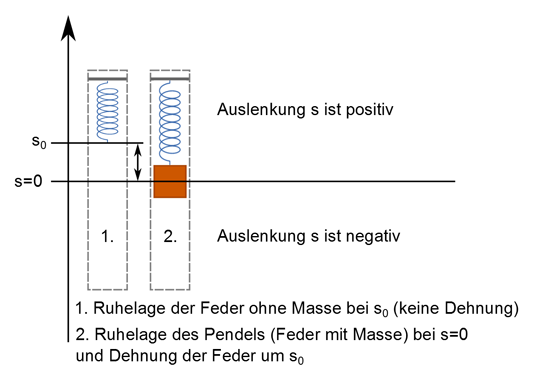
- Der Ruhelage der Feder ohne Gewicht, welche in diesem Fall bei s0 liegen soll.
- Der Ruhelage der Feder mit Gewicht, welche in diesem Fall bei s(t) = 0 liegen soll. (Die Ruhelage der Feder mit Gewicht entspricht der Ruhelage des Pendels.)
Das heißt, die Feder ist in der Ruhelage des Pendels (s = 0) um die Strecke s0 gedehnt.
Folglich kann die Dehnung der Feder relativ zur Auslenkung des Pendels um dessen Ruhelage beschrieben werden mit:
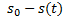
Zum Test: Ist s(t) = 0, also das Pendel in der Ruhelage, so ist die Dehnung gleich s0. Befindet sich das Pendel an der Position s0, so ist die Dehnung der Feder null.
Die potenzielle Energie setzt sich zusammen aus der Höhenenergie und der Federenergie und ist abhängig von der Dehnung der Feder.
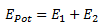
Die Höhenenergie ist gegeben mit:
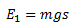
Die Federenergie ist gegeben mit:
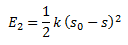Für die potenzielle Energie folgt:
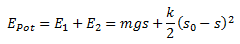
Tipp: Formen Sie den Term für die Federenergie um, bevor Sie weiterrechnen.
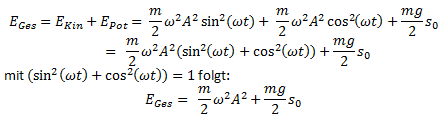
Die Gesamtenergie setzt sich ausschließlich aus verschiedenen Konstanten zusammen und hängt nicht mehr von der Zeit t ab. Dies ist konsistent mit der Formulierung, dass die Gesamtenergie konstant ist und periodisch kinetische und potenzielle Energie ineinander umgewandelt werden.
Erfahrene Studierende und auch theoretische Physiker und Physikerinnen haben neben Zettel und Stift immer auch einen Radiergummi parat. Unabhängig davon, ob Sie die Aufgabe richtig gerechnet haben, überlegen Sie sich, ob Ihnen die Art der Aufgabe zusagt. Im Physikstudium muss viel gerechnet werden. In der theoretischen Physik kommen dabei selten Zahlen vor, es geht vielmehr um die Umformungen von Gleichungen. Auch hier gilt wie im ersten Teil der Aufgabe: Nicht abschrecken lassen - sondern ruhig und strukturiert vorgehen! Dieser Aufgabenteil ist sehr schwer und kann mit Sicherheit oft nicht gelöst werden. Nicht umsonst werden Übungszettel in Kleingruppen abgegeben und die Aufgaben gemeinsam diskutiert. Oft gelangt man nur so zu einem Ergebnis. Auch lohnt es sich manchmal nach ähnlichen Aufgabentypen zu recherchieren und die Lösung dann nachzuvollziehen und auf die eigene Aufgabe anzuwenden. Frei nach dem Motto: "Nicht jedes Rad muss neu erfunden werden, aber man sollte wissen wie es funktioniert."
Macht es Ihnen Spaß komplizierte Rechnungen durchzuführen?
Versuchen Sie die Lösung schwieriger Aufgaben, die Sie selbst nicht lösen konnten, nachzuvollziehen?
Lassen Sie sich von Formeln nicht abschrecken, auch wenn die Formel sehr lang und unübersichtlich erscheint?
Dann ist für Sie das Physikstudium genau richtig!